概述
如果我们要实现一个编解码库,或者通俗的说叫序列化库,用来将内存上的原始数据(对象、结构体等数据实体)编码为便于存储、传输的二进制,首先我们需要分析常见的编程数据实体的构成。
省去具体分析,我们可以知道,编程时的所有数据实体抽象来看,其实都是由如下几种原子类型来编排、组合形成的。
- 数字类型:分为整数、小数
- 字符串类型:顾名思义
- 布尔类型:没有物理上的值,只需要逻辑上二元对立的值即可,数字0和1或者字符串”T”和”F”等都可以
- 表类型:数组、链表
- 字典类型:键值对组成的表
根据上面的类型划分,我们可以知道,表类型、字典类型、布尔类型都是逻辑类型、组合类型,他们的编解码,最终还是落到了数字类型、字符串类型的编解码。
当我们把数字类型、字符串类型数据的编解码搞清楚以后,其他的逻辑类型、组合类型的编解码也就是处理一些边界标识、结构标识等外围工作了。
前一篇【展开讲讲之Unicode字符集和UTF编码】我们详细介绍了字符串编码的概念和技巧,接下来我们再深入研究下数字和数字的编解码小技巧。
数字类型
不纠结佶屈聱牙的数学概念,我们可以把数字分为如下两个大类:
- 整数:没有小数点的数
- 小数:有小数点的数
一堆”数”字看的我都不认识”数”字了
整数
在不同的使用场景下,编程时需要表达的数值的范围是不同的。比如用数字表达ASCII字符的时候,我们只需要表达0-255范围的数值即可、用数字表达Unicode字符时,我们需要0-114w范围的数值。
为了让使用者可以根据使用场景控制数据的存储空间,常用编程语言一般预定义了如下几种不同容量的数字类型:
- int8:1字节,容量为256
- int16:2字节,容量为65536
- int32:4字节,容量为42亿左右
- int64:8字节,容量算不太清了T_T,反正很大
人类能理解的、可读的十进制数值,做进制转换编程二进制,放到上述的宽度的字节序列中,交由计算机理解、处理。
如下图所示,整数31的二进制表达如下:
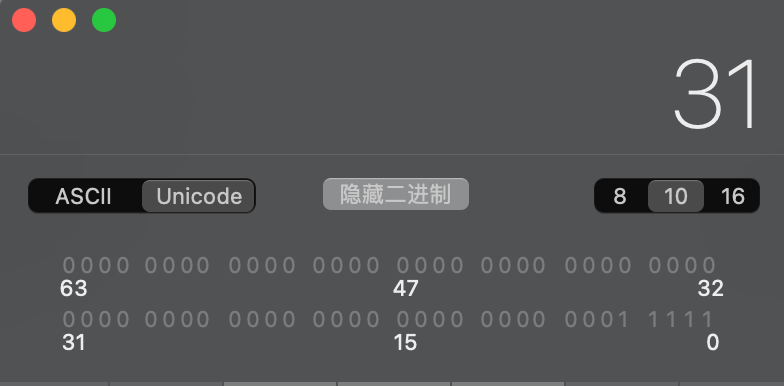
- 使用int8类型时,二进制表示为:
00011111 - 使用int16类型时,二进制表示为:
0000000000011111 - 使用int32类型时,二进制表示为:
00000000000000000000000000011111 - 使用int64类型时,二进制表示为:
0000000000000000000000000000000000000000000000000000000000011111
上述二进制表示,可以放在内存或者寄存器中,可以被CPU指令集中整数相关的指令识别、处理。

小数
小数由两部分组成:小数点前面的部分和小数点后面的部分。二进制表示时,需要同时表达两部分。
它二进制表示有统一的规范【戳我戳我】,分为定点、浮点两种。一方面比较复杂,俺说不清楚,另一方面这块的编解码没啥花头,就内存里的二进制表示是啥样,存储或传输时就啥样就欧了。只是我把数字分类了就都得提一下,这块请大佬们自行领悟吧T_T
为啥小数进行二进制转换、运算后,值会不太对,也跟上述编码规范有关系,具体原因请大佬们自行研究T_T
定点数
浮点数
浮点型的原理介绍及在内存中的存储形式 - 面具下的戏命师 - 博客园
数字编解码
首先编码、解码是一体两面的一个事情,只需要了解其中一块,另外一块就没啥了。
然后,小数的编解码我了解下来都没啥花头,就是按规范的格式原样存储、传输,所以也就不展开了(其实是不会T_T)。
就剩下整数这块在编解码时有一些ROI比较高的优化空间,所以接下来重点介绍这块。
字节序
首先我们要了解一下字节序,但其实字节序不是重点。因为按我理解,字节序的差别跟同一件快递用蓝盒子装还是用绿盒子装的差别一样,其实没啥本质差别,不影响核心的编解码逻辑,但是为了凑点字数,我觉得也可以稍微展开下。
字节序分两种:
- 大端字节序:高位字节在前,低位字节在后
- 小端字节序:低位字节在前,高位字节在后
这里说的高位、低位是相对的,在一个具体的范围内才能看出来高低,也就是需要放在一个具体的编码单元内探讨才有意义。
以61455(0xF00F)这个数字为例,逻辑上的二进制表示为:11110000 00001111
以上述两个字节为二进制单元来看存储、传输时的物理上的二进制表示的话,会有如下结果:
- 大端字节序:
1111000000001111 - 小端字节序:
0000111111110000
也就是说只是改变了一个编码单元内的字节排列顺序而已,别的也没啥。
只是需要注意,因为字节序这块已经有了并行的两套用法,那么在制定编码、传输协议或者使用编码、传输协议时,协议使用的字节序就是一个需要明确说明的点,避免歧义。
CPU指令集是CPU使用者和CPU设计者之间的二进制交互协议,所以指令集也需要指明字节序哦
Varint
以int32宽度整数为例,一个数在内存里占32bit。如果数字很小,那二进制下的bit序列会有大量的前导0。
如数字1,当使用int32来分配内存时,内存上的bit布局如下:
00000000 00000000 00000000 00000001
前导0在传输时是可以省去的,因为收到数据后直接补0到指定长度即可,不会影响数据。所以如果在传输时,直接原样传输上述32bit,其实是有很大浪费。
所以可以想办法,在传输int32时,不传输定长的32bit,而是根据数值的具体值,传输一个省略前导0的边长二进制序列。上述数值1,就可以只传输00000001。从而实现精炼、高效的传输。
编码单元变长带来了和tcp半包、粘包一样的问题:如何确定编码单元边界?
按tcp拆包的思路,变长报文的协议中,要么加一个固定的分隔符,要么加一个字段提示报文长度来便于拆包。
上述思路不适用于数字编码,因为变长编码压缩出来的空间还不够分隔符用的T_T。
但是可以得到的一点启示就是,边长编码拆包的关键是在编码时加入编码单元分界提示。
varint的核心原理就是,一个编码单元产生的多个字节,最后一个字节第一bit是0,其他字节的第一bit是1。
在拆包时,从前往后读字节,一直读到第一bit为0,就知道当前编码单元的所有字节读完了,即完成了拆包。
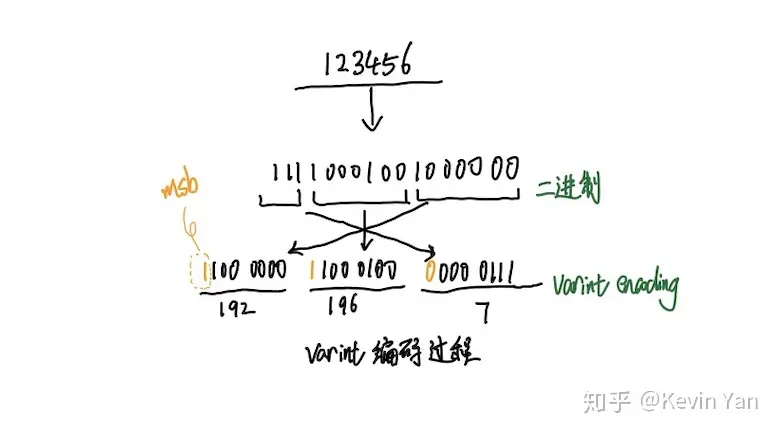
上图可以看出,varint编码时小端字节序编码~
通过上述方式,实现了整数的变长编码,相对于int32原始的32bit定长编码,大数用的字节更多,小数用的字节更少。这也需要使用时评估,如果使用场景下的数值普遍都很大,那就不适用这种编码优化了,因为相对于32bit定长编码,使用的字节更多了。所以varint的编码优化也是有其适用场景,它不是银弹~
UTF8编码其实也是类似varint的变长整数编码协议,大佬们可以对照着瞅瞅。
Zigzag
varint实现了数字的变长编码,其核心是在存储、传输过程中丢弃了二进制序列中无用的前导0。
但是,当编码的数字是负数时,就不太给力了。
我们知道,为了实现加减法运算的统一,复用cpu运算单元,负数的二进制表示是其逻辑二进制序列的补码。
以int32类型的-1为例,它逻辑上的二进制序列为:-00000000 00000000 00000000 00000001。
但是物理上的二进制序列为其补码表示:11111111 11111111 11111111 11111111。
大佬们一看就发现了,这个二进制序列里没有无用的前导0,如果直接用varint编码,反而会使用比32bit更多的字节。 得想想办法才行!机智的前辈们摸摸头皮想了想,有了一个好主意。
我们以int8为例,其一共256的容量,一半为整数,一半为负数。
按补码规则,0xxxxxxx 这一段表示整数,1xxxxxxx这一段表示负数。
负数一直有一个在传输中不能丢弃的前导1,假设我们想个办法建立一个如下映射表:
| 映射索引值 | 映射原始值 |
|---|---|
| 0 | 0 |
| 1 | -1 |
| 2 | 1 |
| 3 | -2 |
| … |
在存储、传输时,我们不传输原始值,只传输原始值在上述映射中的索引,在使用时,我们查上述索引表来恢复具体原始值。
这样映射后有个好处,以-1来说,他的索引值变成了1,二进制序列为00000000 00000000 00000000 00000001。看到那么多前导0,是不是DNA开始动了?
是的,又可以用varint来压缩处理了。
上面的分析都挺好,就是有一点不太好处理,怎么保证读写两端有一个一致的映射表呢?映射表那么大,不是也会占用大量空间?
hhhh,其实上面那个只是一个自相关的、逻辑上的映射表,不需要被物理存储、共享。
因为索引值和原始值存在一个可逆的一一对应的换算关系:


代码截图来自protobuf源码
也就是说,上述映射表无需读写两端传输、共享,没有引入太多复杂度,开销可控(cpu工作量会更饱和一些)。
图形化的看一下上述那个逻辑映射表如下:
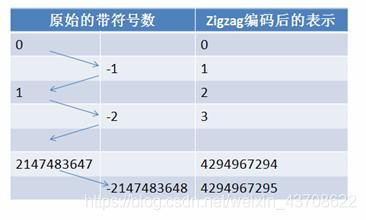
正数、负数在映射索引上是来回往复映射的,像”之”字形,这也是zigzag(之字形,锯齿形线条)命名的由来。
总结
重点介绍了整数的编码优化,主要有varint、zigzag两种方式。
具体使用场景如下:
- 绝对值比较小的无符号数:用varint
- 绝对值比较大的无符号数:定长传输即可
- 绝对值比较小的有符号数:先zigzag转成无符号数,然后在用varint
- 绝对值比较大的有符号数:定长传输即可
大佬,你学废了嘛?